The evolution of cooperation among animals, either within or between species, presents an obvious problem for Darwinists. Darwin himself recognised this. He thought that social behaviour, as shown by social insects, could be explained by family selection. He also remarked that his theory would be disproved if it could be shown that some property of one species existed solely to ensure the survival of another; by implication, mutualism between species must be explained by indirect benefits to the individuals performing cooperative acts.

Despite these essentially correct insights, little progress was made in analysing the selective forces responsible for the evolution of cooperative behaviour for 100 years after the publication of The Origin of Species. For many biologists, it was enough that a trait could be seen to favour the survival of the species, or even of the ecosystem. It is clear from the writings of J. B. S. Haldane and R. A. Fisher that they knew better than this. The decisive turn to the significance of kinship in social behaviour, however, was by Hamilton (1964). Perhaps inevitably, the elegance of the idea of inclusive fitness and the prevalence of genetic relationship between members of social groups tended to distract attention from other selective forces, and in particular from mutualistic effects; that is, from the fact that two (or more) individuals may cooperate because it benefits both to do so. However, the significance of mutualistic effect was not lost sight of (e.g. Michener, 1974; West-Eberhard, 1975), and Trivers (1971) pointed out the possibility of delayed reciprocation.

Today it is clear that the evolution of social behaviour has involved both interactions between kin, and mutual benefits to cooperating individuals. In this chapter, I want to approach the problem from a different direction, although the conclusions reached will be similar. I start by describing the work of Axelrod (1981) on the evolution of cooperation in the Prisoner’s Dilemma game. Then, following Axelrod & Hamilton (1981), I discuss how Axelrod’s ideas might be relevant to animal evolution. Finally, I turn to the problem of human cooperation, and the possible relevance of evolutionary game theory to cultural evolution.

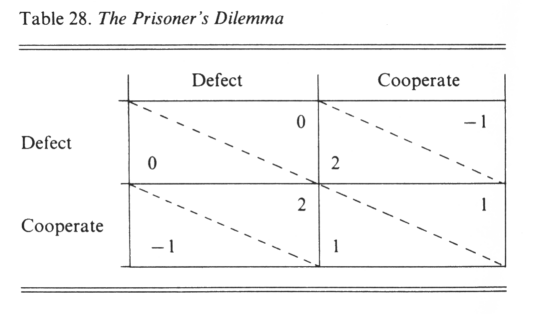
The Prisoner’s Dilemma is a symmetric two-person game, in which the alternative plays are ‘Cooperate’ and ‘Defect.’ The payoffs are shown in Table 28, p. 162. Note that if player B cooperates, it pays A to defect; also, if player B defects, it pays A to defect. That is, it pays A to defect no matter what B does; similarly, it pays B to defect no matter what A does. Yet, if both defect, they do less well than if both cooperate; this is the paradox.

Considered in an evolutionary context, if each individual plays only a single game against each opponent, the only ESS is to defect. Cooperation will not evolve. Things are different, however, if individuals play repeatedly against the same opponent; it is this situation which Axelrod has studied. He invited a number of people to contribute a computer program to play the Prisoner’s Dilemma repeatedly against the same opponent. He then ran a tournament between the programs submitted, each program playing 200 games against each other one. The programs were then ranked according to the total payoff accumulated (not, it should be noted, according to the number of opponents defeated in the individual matches). The winning program, submitted by Anatol Rapoport, was also the simplest. It was ‘TIT FOR TAT’; it chooses Cooperate on the first move, and on all subsequent moves makes the choice adopted by its opponent on the previous move.

The results of this tournament were published, and people were invited to submit programs for a second tournament. This was identical in form to the first, except that matches were not of exactly 200 games, but were of random length with median 200; this avoids the complication that programs may have special rules for the last game. Again, TIT FOR TAT was the winner. Further computer analysis showed that if a succession of tournaments were played, with programs increasing in representation if they did well, then TIT FOR TAT ultimately displaced all others. That is, for the programs submitted, TIT FOR TAT was an ESS.

What properties make TIT FOR TAT an ESS? Axelrod suggests that a successful strategy must be ‘nice,’ ‘provokable’ and ‘forgiving.’ A nice program is one which is never the first to defect. In a match between two nice programs, both do well. A provokable strategy responds by defecting at once in response to defect; a program which does not at once respond in this way encourages its opponent to defect. A forgiving strategy is one which readily returns to cooperation if its opponent does so; unforgiving strategies are likely to get involved in prolonged periods in which both defect.

Axelrod has later been able to prove that TIT FOR TAT is stable against invasion by any other possible strategy, provided that the sequence of games against each opponent is long enough; his proof is summarised in Appendix K. However, TIT FOR TAT is not the only ESS. Thus ‘Always defect’ is an ESS. A comparison of TFT = TIT FOR TAT and D = Always defect shows that the former has a much wider basin of attraction. Thus suppose that individuals play mainly against their neighbours, and that there is some clustering of individuals with similar strategies. It then turns out that TFT, even when rare, can invade D, because TFT does well against neighbours with the same strategy; clustering does not enable D to invade TFT. This illustrates the fact that kin selection is often needed for the initial spread of a trait which, once it is common, can be maintained by mutualistic effects alone.

These results provide a model for the evolution of cooperative behaviour. At first sight, it might seem that the model is relevant only to higher animals which can distinguish between their various opponents. Thus if such distinction was not possible, an individual which met defection from one opponent would defect against others, and the result would soon be general defection. Axelrod & Hamilton (1981) point out, however, that the model can be applied if each individual has only one opponent in its lifetime. With this proviso, TIT FOR TAT can evolve as a strategy in completely undiscriminating organisms. They also point out that the model can be applied to interactions between members of different species.

If cooperation, within or between species, is to evolve by this road, there are three requirements:

(i) There must be repeated interactions between the same pair of individuals (or, conceivably, between two clones or two endogamous groups).

(ii) Each partner must be able to retaliate against defection by the other.

(iii) Either individual recognition must be possible, or the number of potential partners with whom an individual interacts must be small, preferably only one.

Axelrod & Hamilton discuss various examples of cooperation and its breakdown from this point of view. First, many examples of mutualism involve interactions between one member of one species and one of another, as for example in sea anemone and hermit crab, or tree and mycorrhizal fungus. Sometimes the number of interacting partners is effectively limited by interacting at a particular site, as in the cleaning fish discussed by Trivers (1971).

The possibility that cooperation may evolve, not between individuals, but between endogamous groups has been discussed by D. S. Wilson (1980; for a mathematical treatment, see Slacken & Wilson, 1979) under the term ‘indirect effects’; although he does not explicitly refer to endogamy, it is clear that the mechanism he has in mind requires a high degree of population viscosity between generations. As an example, Axelrod & Hamilton point to the fact that ant colonies participate in many symbioses, whereas honey bees, which move from place to place more frequently, have many parasites but no known symbionts.

In higher organisms, cooperation can depend on individual recognition. Perhaps the clearest example is Packer’s (1977b) demonstration of reciprocal altruism between pairs of male olive baboons, in the absence of any known genetic relationship between the interactants. As argued on p. 164, reciprocal altruism of this kind can readily be modelled as a game, with TIT FOR TAT as the ESS.

Applying these ideas to baboons, and a fortiori to men, raises questions about the nature of the ‘hereditary’ mechanism – genetic or cultural – underlying the evolutionary process. Thus the conclusion that cooperative behaviour is a stable outcome rests on the assumption that individuals who are in some sense successful pass their characteristics on to more ‘descendants’ than those who are not. Three hereditary mechanisms are conceivable:

(i) Genetic. The assumption is that differences between individuals adopting different strategies are, at least in part, genetic: i.e. caused by differences between the fertilised eggs from which they developed. It seems to me important that terms such as ‘genetically determined’ or ‘innate’ should be used in this rigorous sense. This has by no means always been the case in discussions of sociobiology. For example, E. O. Wilson (1978) starts the chapter on aggression as follows: ‘Are human beings innately aggressive? This is a favourite question of college seminars and cocktail party conversations, and one that raises emotion in political ideologues of all stripes. The answer to it is yes.’ Yet it turns out, on reading the rest of the chapter, that the only proposition Wilson defends is that human beings are sometimes aggressive.

It seems unlikely that the reciprocal altruism in baboons, discussed by Packer, is maintained solely by selection acting on genetic differences. Some degree of imitation, and perhaps insight learning (i.e. a calculation of the costs of not reciprocating), are probably also involved. In man, such processes are likely to predominate. Nevertheless, genetic evolution may have made both baboons and people readier to learn some things than others.

(ii) Learning. In Chapter 5, it was shown that a generalised learning rule, not specific to any particular game or problem, can take a population to an ESS in one generation. But such a learning rule cannot help much in the present context. Thus the type of learning rule which was discussed had, as its starting point, a set of possible ‘behaviours.’ In the context of a repeated Prisoner’s Dilemma, this would require that an individual start with a set of possible strategies, of which TIT FOR TAT would be one; that he play a succession of long matches against individual opponents, adopting different strategies for different matches; and that he gradually adjust the frequencies of the different strategies in accordance with outcomes. One lifetime would not be long enough for such an inefficient learning process.

For man, one can consider the alternative possibility of insight learning. A man might imagine a series of matches, adopting different strategies, and thereby calculate that TIT FOR TAT was best. This also seems implausible; the scientists who participated in Axelrod’s tournaments were apparently unable to perform this calculation.

Learning would, however, be important in maintaining TIT FOR TAT, once established. Thus if almost everyone is playing TIT FOR TAT, it would not pay an individual to adopt any other strategy. This could readily be learnt by trial, either in practice or in imagination.

(iii) Cultural inheritance. Suppose, to take an oversimplified model, that individuals acquire their behaviour by learning or imitation from others, and that they are more likely to copy successful mentors. Such a process of cultural inheritance would lead to the spread of behaviour patterns, including cooperation, which meet the criteria of evolutionary stability. Such processes of cultural inheritance, and their interaction with genetic processes, have been discussed in much greater depth by Feldman & Cavalli-Sforza (1976) and Lumsden & Wilson (1981). My only purpose here is to raise the question of what types of cultural heredity would be formally similar to asexual genetic inheritance, in the sense of leading to evolutionarily stable states.

I am, in fact, more interested in raising this question than in solving it. Game-theoretic ideas originated within sociology. Naturally enough, the solution concepts which developed were based on the idea of rational calculation. The ideas were borrowed by evolutionary biologists, who introduced a new concept of a solution, based on selection and heredity operating in a population. If, as seems likely, the idea of evolutionary stability is now to be reintroduced into sociology, it is crucial that this should be done only when a suitable mechanism of cultural heredity exists.

It may be that cultural processes will often mimic genetic ones; but there is one distinction which needs to be made between kinds of cultural inheritance. First, consider a case in which all children acquire some trait by imitating their mothers, and in which mothers pass on the trait which they themselves acquired. In the evolution of such traits, ‘fitness’ would be measured by the Darwinian fitness of mothers; those traits would increase which enabled their possessors to survive and have more children. At the opposite extreme, suppose that each child acquires some trait by imitating a mentor who is not a parent, but who is judged to be ‘successful’ by some criterion. Traits will then increase which ensure ‘success,’ however that is measured. Since the criteria of success are themselves to some degree culturally determined, a much more complex, but perhaps more realistic, process is involved.

I have written so far as if behavioural traits are properties of individuals, and as if individuals acquired a behaviour for life. Neither of these things is true. Individuals may change their behaviour, and horizontal as well as vertical transmission can occur. Some customs and practices may be properties of institutions – firms, schools, regiments etc. – and at least some such institutions may grow at rates determined by their practices.

In conclusion, there is at least one kind of game which people play, but which seems beyond the capacity of animals. This is the ‘social contract’ game. Thus suppose that some pattern of behaviour – for example theft – is seen to be undesirable. A group of individuals capable of symbolic communication can agree not to steal, and to punish any member of the group who does steal. That, by itself, is not sufficient to guarantee stability, because the act of punishing is presumably costly, and therefore individuals would be tempted to accept the benefits of the contract but not the costs of enforcing it. Stability requires that refusal by an individual to participate in enforcing the contract should also be regarded as a breach which will be punished. At a later stage, enforcement is entrusted to a subgroup, who are rewarded for carrying it out.